▶ 퍼셉트론
- 다수의 신호를 입력으로 받아서 하나의 신호를 출력함
- 뉴런에서 보낸 신호의 총합이 정해진 한계(임계값)를 넘어설 때만 1을 출력함(이 때 뉴런이 활성화된다고 함)
- AND 게이트
- 입력이 둘이고 출력은 하나인 논리 회로임
- 두 개의 입력이 모두 1일 때만 1을 출력함

- NAND 게이트
- Not AND를 의미함
- 즉, AND 게이트의 출력을 뒤집은 것임
- 마찬가지로 입력이 둘이고 출력은 하나인 논리 회로임
- 두 개의 입력이 모두 1인 경우에만 0을 출력하고, 나머지 경우는 모두 0을 출력함

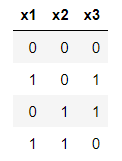
- OR 게이트
- 마찬가지로 입력이 둘이고 출력은 하나인 논리 회로임
- 입력 신호 중, 하나 이상이 1이면 출력이 1이 됨

import numpy as np
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5]) # AND와는 가중치(w와 b)만 다르다.
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # AND와는 가중치(w와 b)만 다르다.
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
여기서 중요한 점은 퍼셉트론의 구조는 AND, NAND, OR 게이트 모두에서 똑같다는 것이다.
위 세 가지 게이트에서 다른 것은 매개변수(가중치와 임계값) 뿐이다. (여기서 임계값을 "편향"이라고 볼 수 있다)
즉, 퍼셉트론에서는 "가중치"와 "편향"을 매개변수로 설정하고, 이 값들만 적절히 조정해서 AND, NAND, OR로 변하는 것이다.
- XOR 게이트
- 배타적(즉, 자기 외에는 거부) 논리합이라는 논리 회로임
- 두 개의 입력 중, 한 쪽이 1일 때만 1을 출력함
- XOR 게이트는 직선 하나로 나누기가 불가능함 (즉, 단층 퍼셉트론으로는 표현이 불가능)
import numpy as np import matplotlib.pyplot as plt import matplotlib x1 = np.arange(-1, 3, 0.1) x2 = -x1 + 0.5 plt.axvline(x=0, color = 'b') # draw x =0 axes plt.axhline(y=0, color = 'b') # draw y =0 axes # 그래프 그리기 plt.plot(x1, x2, label="or") plt.xlabel("X1") # x축 이름 plt.ylabel("X2") # y축 이름 plt.legend() plt.fill_between(x1, x2, -3, color='grey', alpha='0.5') plt.scatter([0],[0],marker='o',color='r') plt.scatter([1,0,1],[0,1,1],marker='^',color='r') plt.show()
정리하면 단층 퍼셉트론은 직선형 영역만 표현할 수 있지만, 다층 퍼셉트론을 사용하면 비선형 영역도 표현할 수 있다.
'Deep Learning > 밑바닥부터 시작하는 딥러닝' 카테고리의 다른 글
| DL - #5-1, 오차역전파법 (0) | 2022.02.04 |
|---|---|
| DL - #4 -2, 신경망 학습 (0) | 2022.02.04 |
| DL - #4 -1, 신경망 학습 (0) | 2022.02.04 |
| DL - #3, 신경망 (0) | 2022.02.04 |
| DL - 퍼셉트론 정리 (0) | 2022.01.27 |